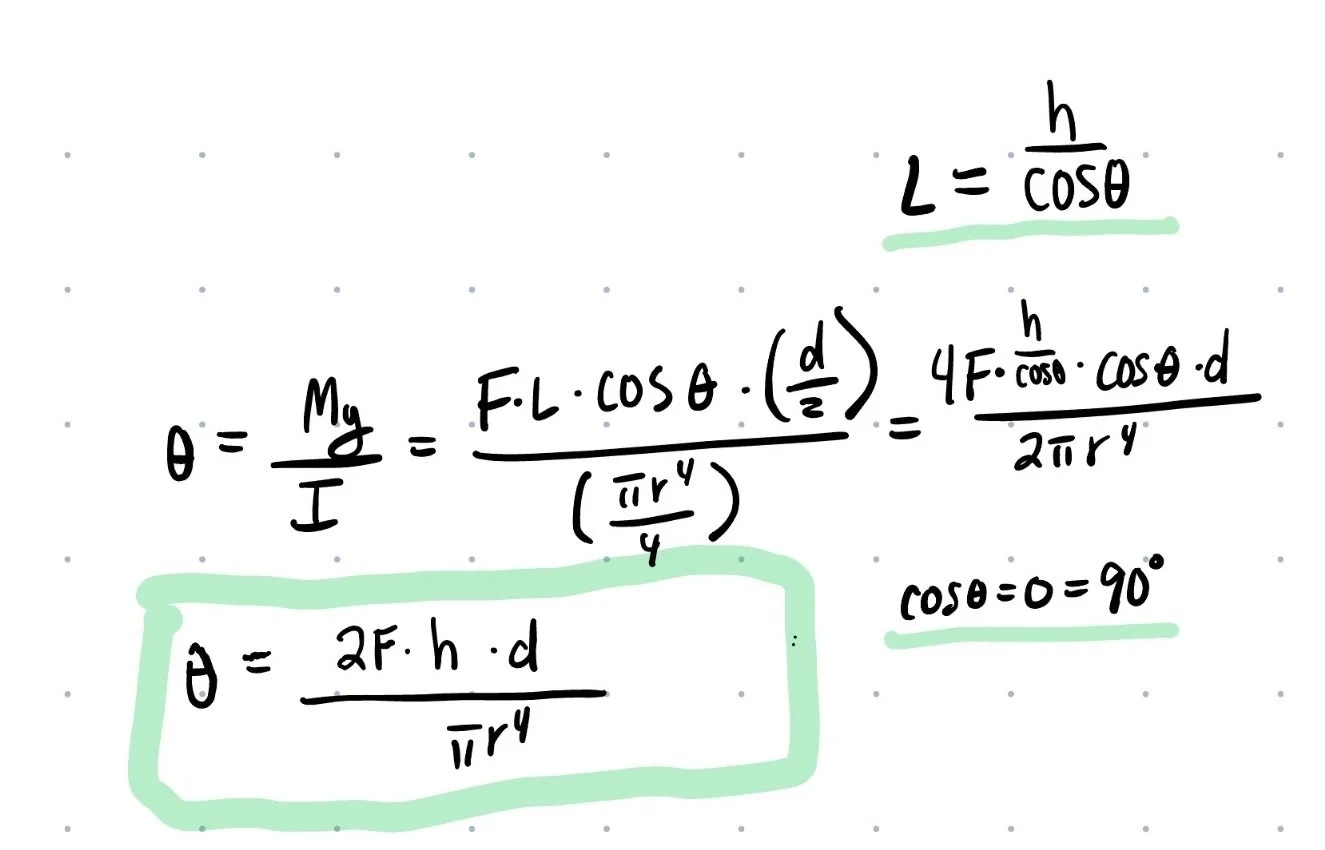Martian Banana Beam
For: Stanford University
Class: ME 104 - Mechanical Systems Design - Winter 2025
Length: 3 Weeks
Materials: 3D Printed PLA
Skills: CAD/Fusion 360, Structural Analysis, Finite Element Design (FEA), Design for Mass Efficiency, Additive Manufacturing, Iterative Prototyping, Performance Testing
Type: Individual Project
Goals: Designing, analyzing, 3D-printing, and testing a lightweight structural PLA component that fits within specific geometric constraints, withstands a ≥ 200 N load with ≤ 0.010 m deflection, and is optimized for mass efficiency.
Why?
To design and optimize a lightweight, high-strength structural component under strict geometric, load, and material constraints
To strengthen skills in mechanical analysis, CAD/FEA simulation, and iterative prototyping through design, 3D printing, and performance testing
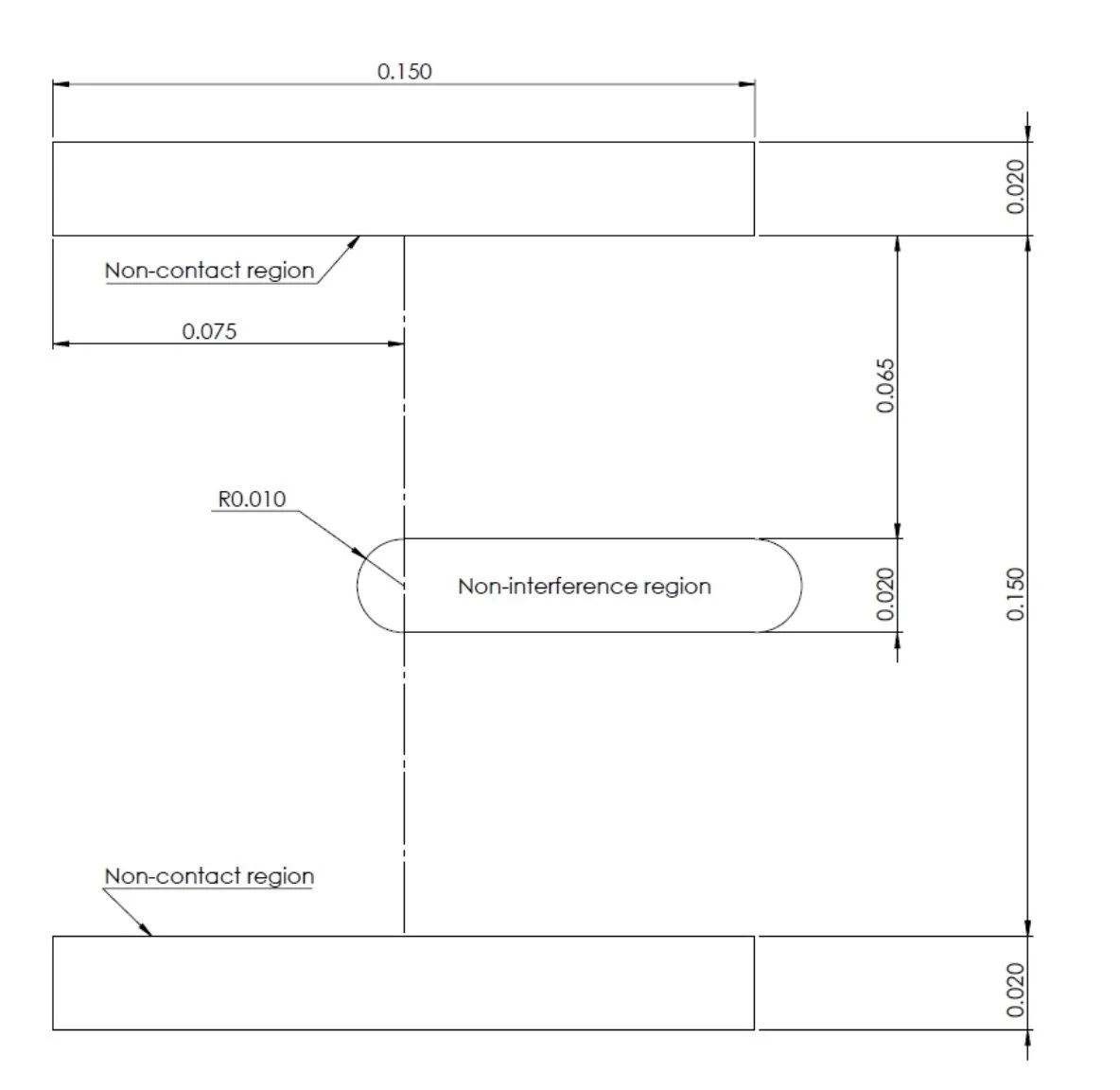
Constraints:
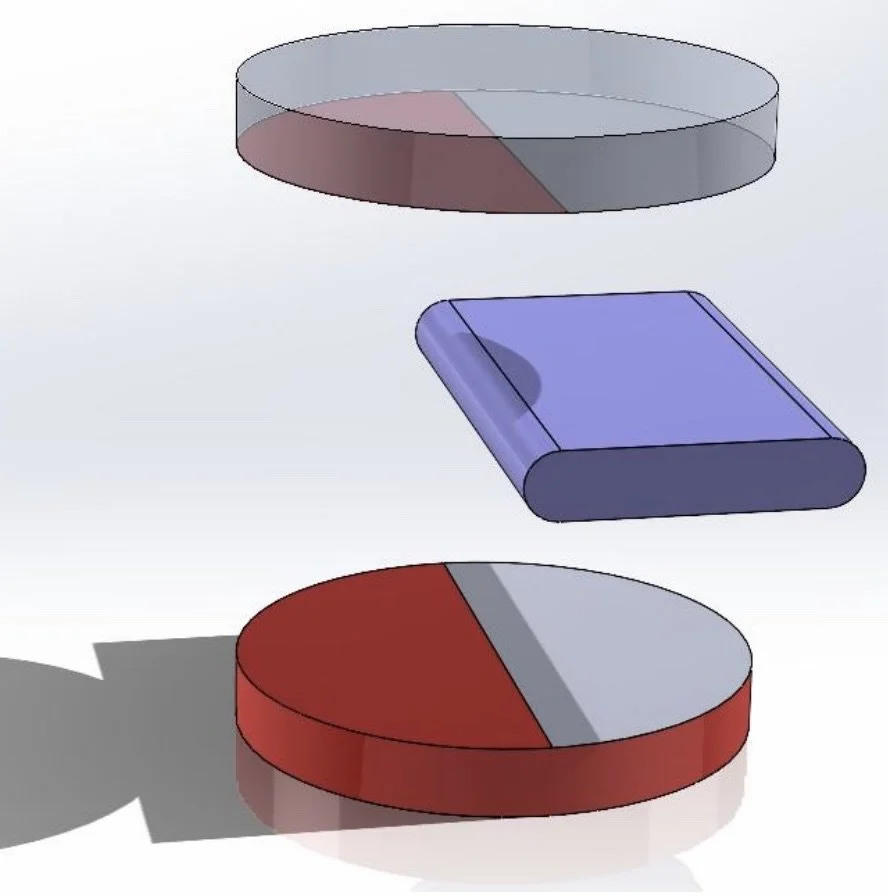
Candidate Shape
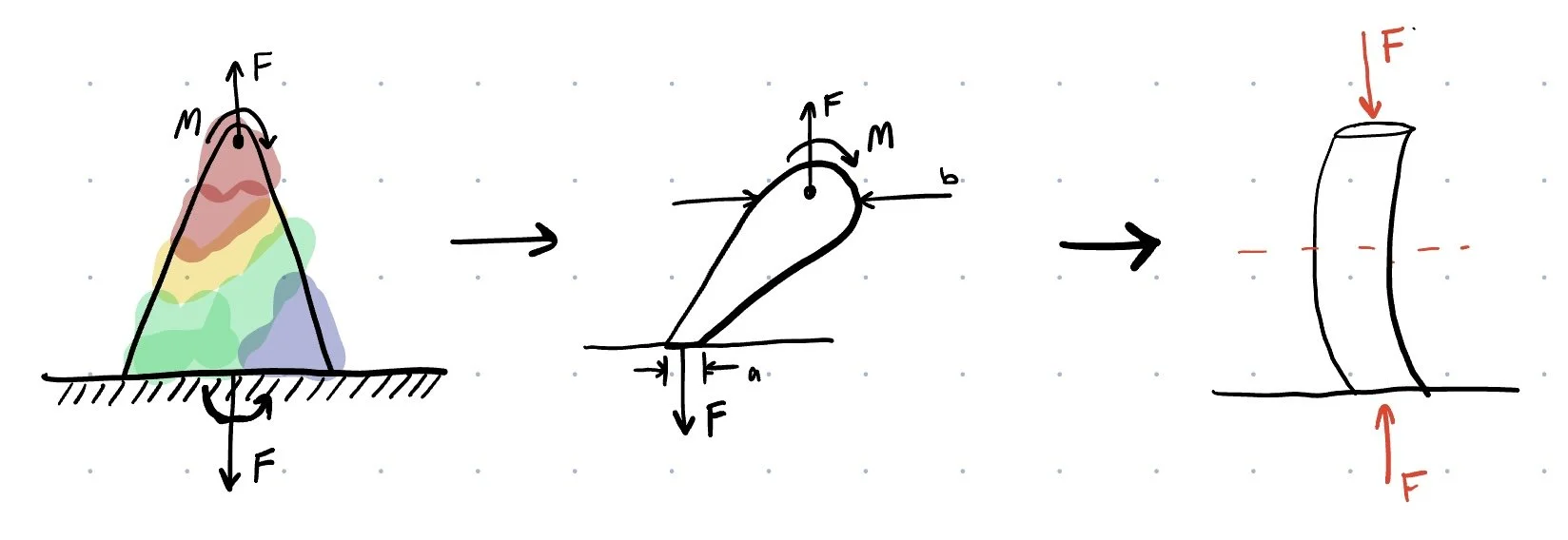
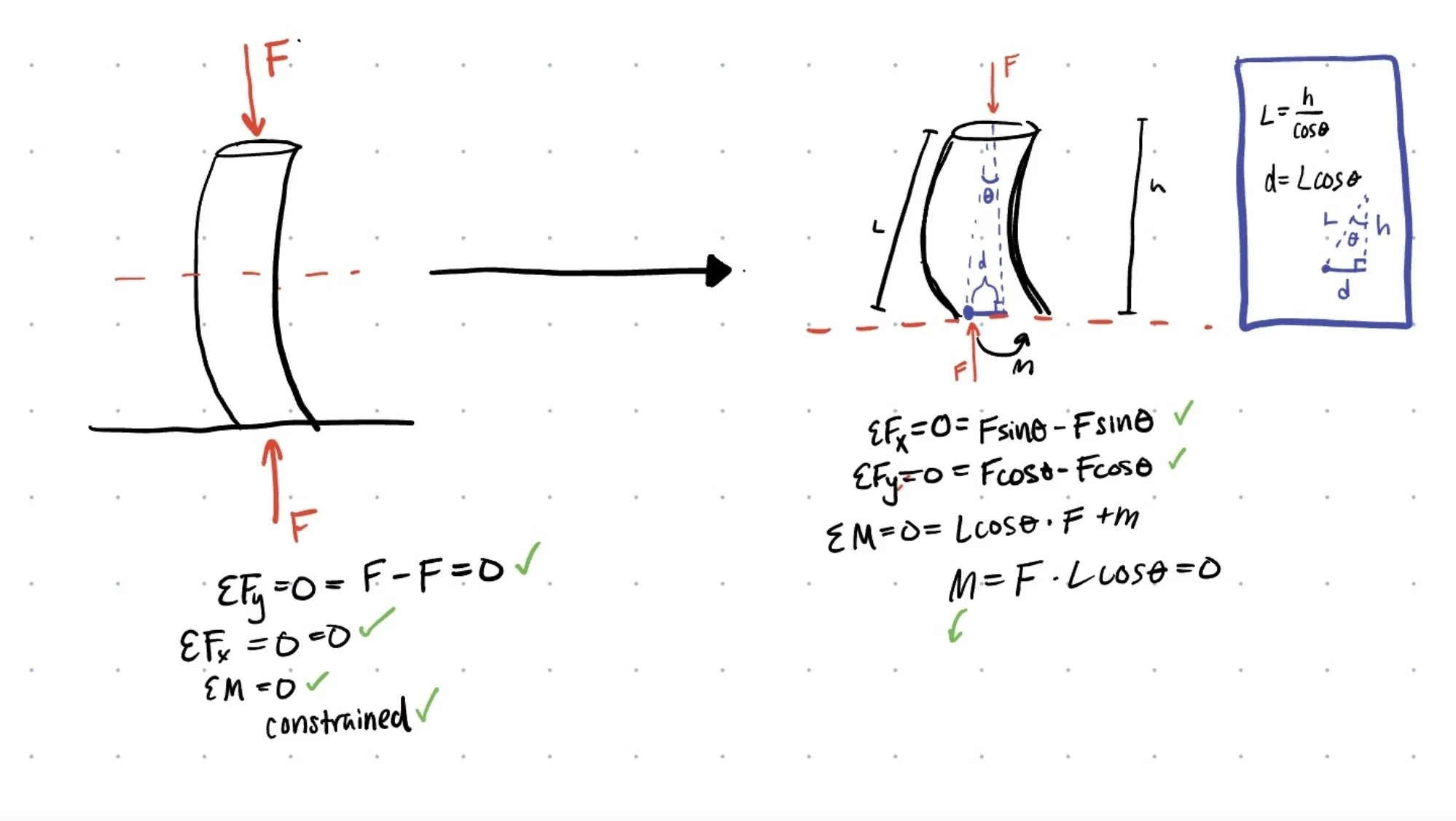
Free Body Diagrams
Wants
Thicker build when the Moment increases in the middle of the structure
Axial Stress Analysis and Inverse
Shows that the larger the radius, the smaller the axial stress
Most concerned about bending and buckling analysis
Analysis:
Bending Stress Analysis
Shows that theta needs to be as close to 90 degrees as possible for least amount of buckling
Analysis:
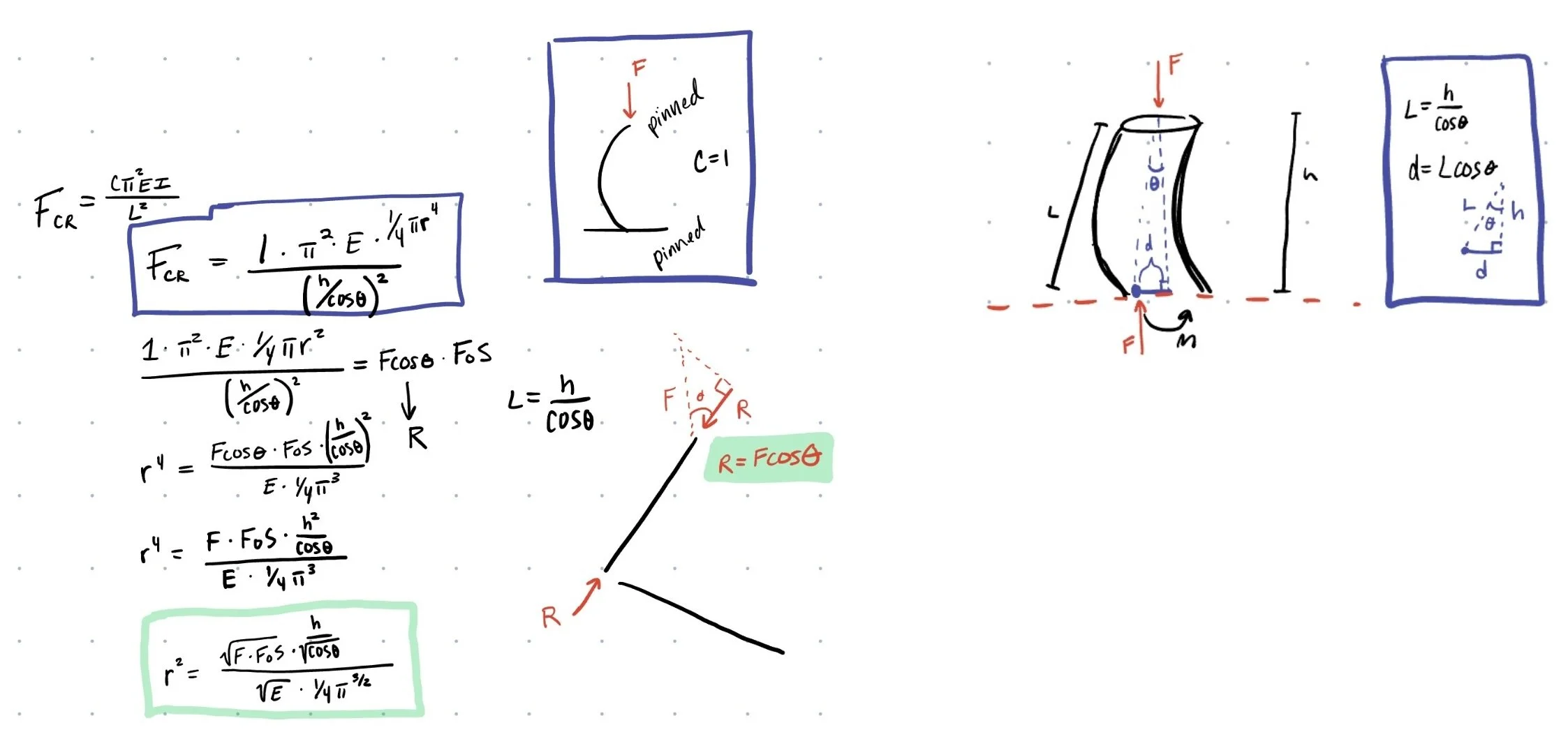
Buckling Stress Analysis and Inverse
By inverting Euler’s buckling equation, this analysis links load requirements, geometry, and material properties to the minimum radius needed for stability — ensuring the design resists buckling with an appropriate factor of safety while remaining mass-efficient
Analysis:
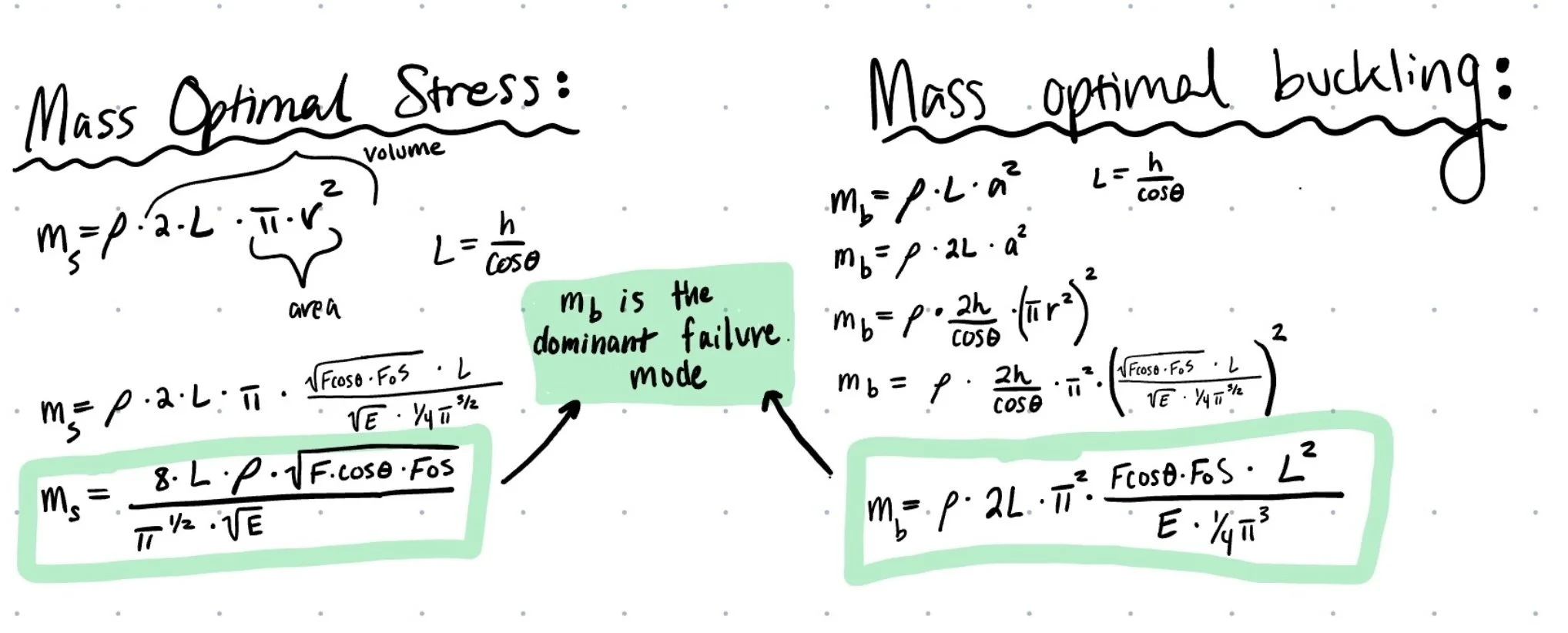
Mass Optimal Stress & Buckling
Mass optimal buckling is the dominant failure mode
Analysis:
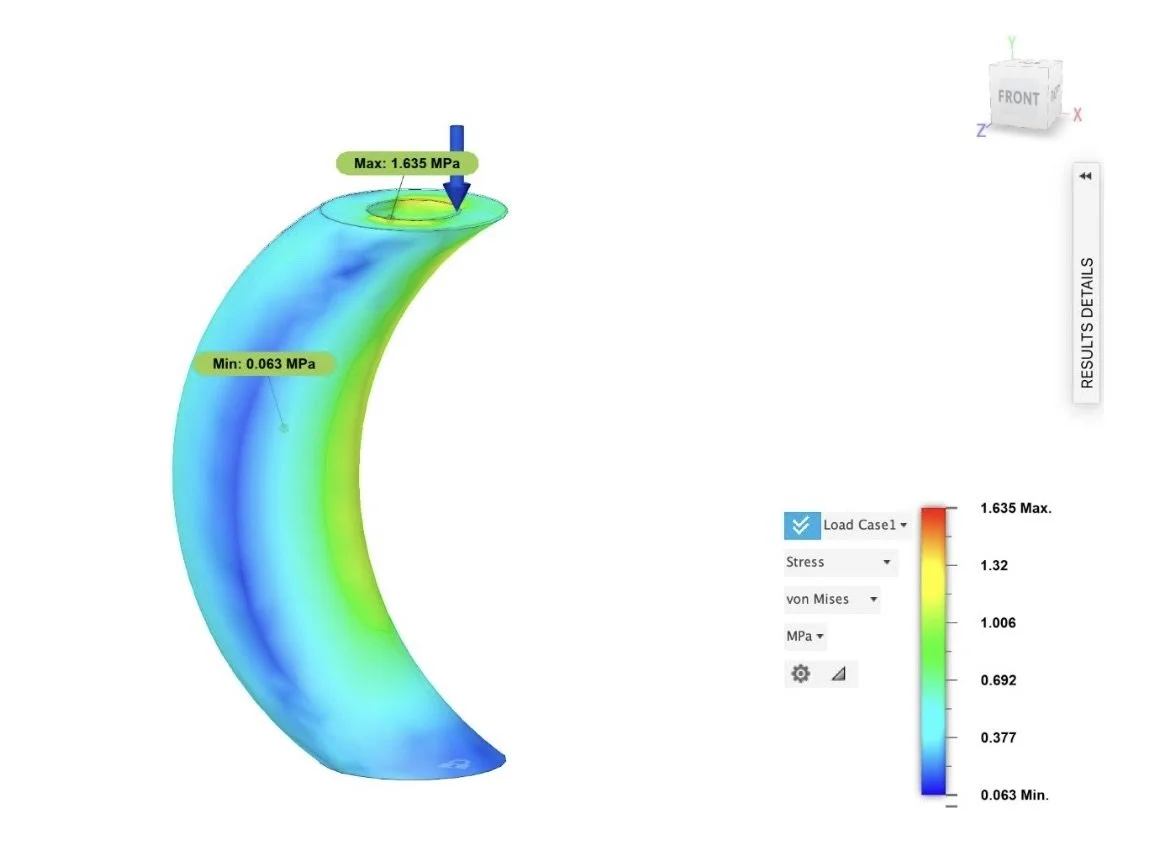
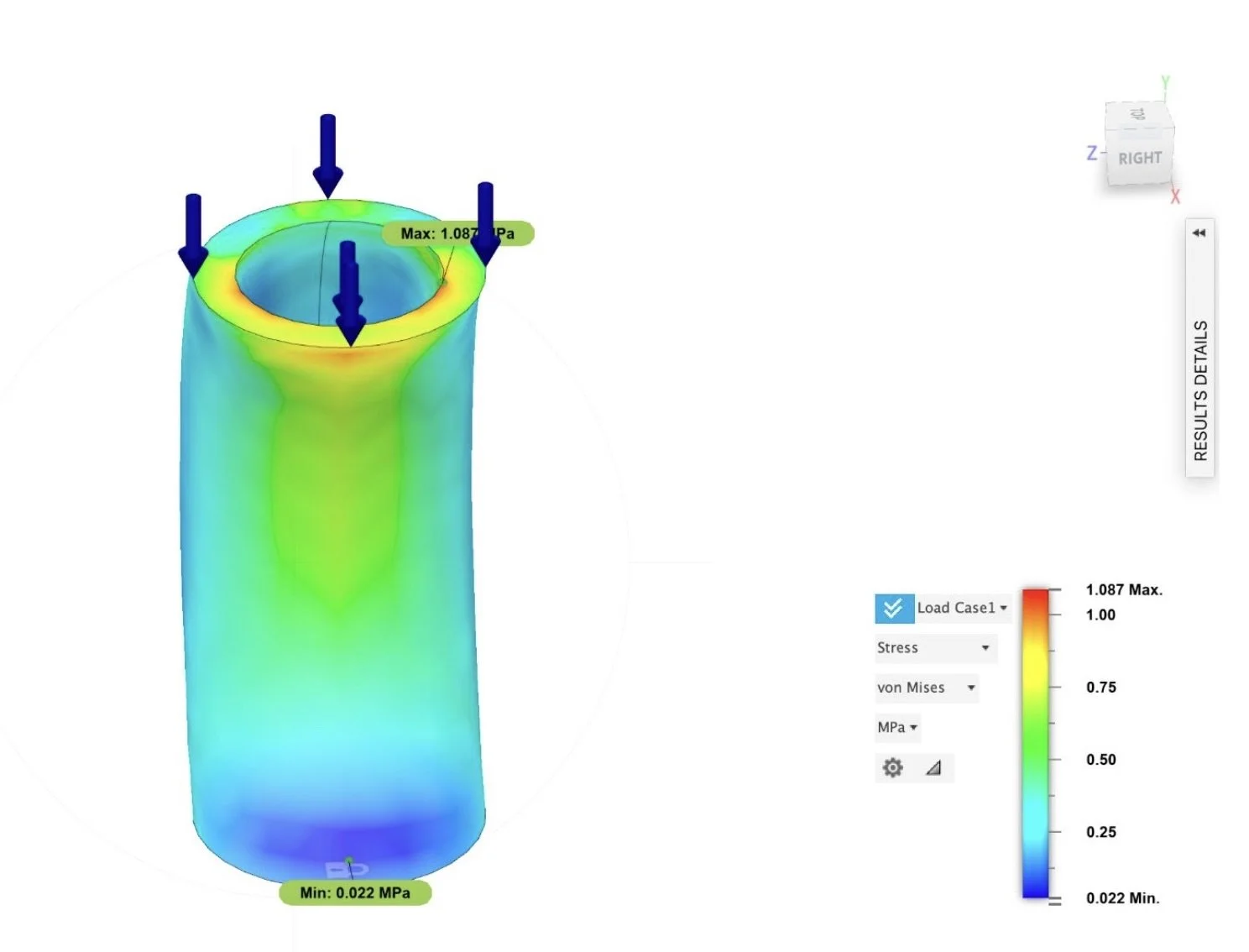
FEA Analysis
5 cm outer diameter
2.5 cm inner diameter
7.5 cm outer diameter
5 cm inner diameter
More stress/less evenly distributed
Summary:
Add mass in the middle
Shrink the radius of the ends
Make theta as close to 90
Keep the tube/cylindrical shape /no corners
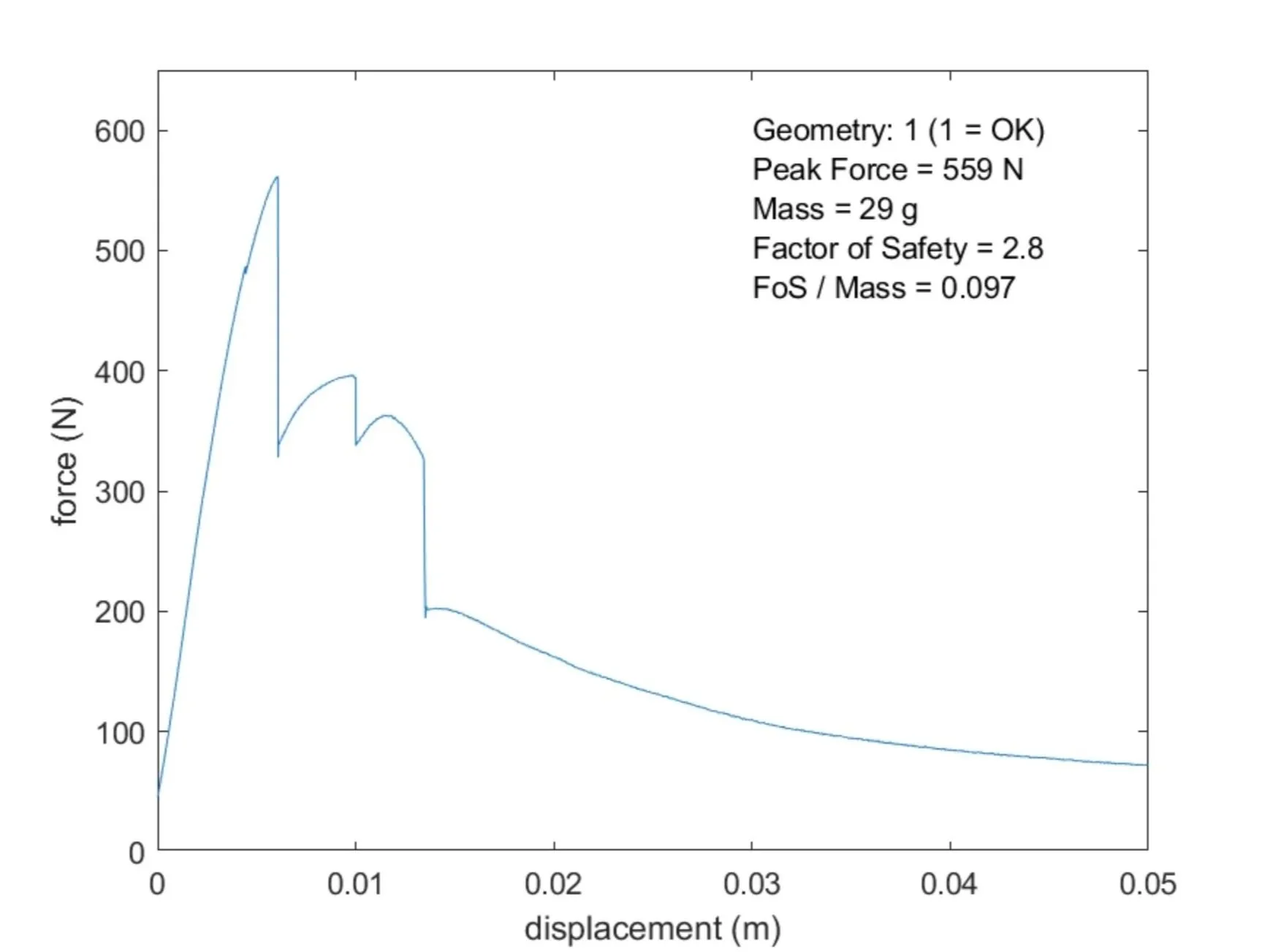
Testing Day
Passed!
Alterations for next time:
Further minimize mass